John Venn
(Drypool, 1834 - Cambridge, 1923) Matemático y lógico británico a quien se deben los diagramas que llevan su nombre.

John Venn
Miembro de una familia piadosa, a los veinticinco años se ordenó sacerdote y desde 1862 ejerció la docencia como profesor de lógica y filosofía de la ciencia en Cambridge, donde residiría hasta su fallecimiento. Hacia 1883, sin embargo, abandonó el sacerdocio por considerar incompatible el anglicanismo con sus creencias filosóficas.
Considerado uno de los creadores de la lógica matemática, John Venn descolló por sus investigaciones en lógica inductiva. Es especialmente conocido por su método de representación gráfica de proposiciones (según su cualidad y cantidad) y silogismos. Los diagramas de Venn permiten, además, una comprobación de la verdad o falsedad de un silogismo.
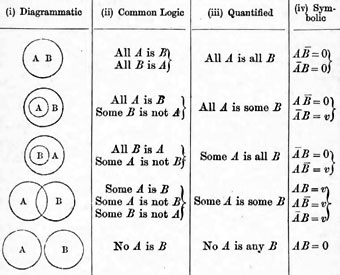
Representación de proposiciones con diagramas de Venn (tabla incluida en su obra Lógica simbólica, 1881)
Posteriormente, y gracias a su claridad y sencillez, sus diagramas se popularizaron y fueron utilizados para mostrar visualmente las operaciones más elementales de la teoría de conjuntos, desarrollada desde 1874 por Georg Cantor a partir de las ideas de Bernhard Bolzano y perfeccionada, ya en el siglo XX, por Ernst Zermelo.
Entre las obras de John Venn destacan La lógica del azar (1866), que versa sobre la teoría de las probabilidades; Lógica simbólica (1881), que incluye sus célebres diagramas, y Los principios de la lógica empírica o inductiva (1889). Curiosamente, en sus últimos años no profundizó en tales materias, sino que se dedicó a estudiar la historia del colegio en que se formó y de la Universidad de Cambridge, así como la de su propia familia.
Tomado de:
Tomado de:




+%E2%88%A9+(A+%E2%8B%83+C).png)
